统计学习方法笔记第二篇。今天进行整理的是CART(Classification And Regression Tree)算法。同C4.5相似,CART同样包含特征选择,树生成和剪枝等步骤。CART主要有两点不同:
- 决策树是二叉树,相当于递归地二分特征空间;
- 对回归树使用最小二乘准则,对分类树使用Gini指数或Towing准则进行特征选择
CART回归树
特征选择准则
在训练集的输入空间中,使用平方误差最小化准则,递归地将每个区域划分为两个子区域并决定每个子区域的输出值,构建最小二乘回归树
生成步骤
给定$X\in R^J$,$Y$为输入和输出变量,其中$Y$为连续变量;训练集$D={(x_1,y_1),(x_2,y_2),…,(x_N,y_N)}$
- 选择最佳切分变量$j$和切分数值点$s$,通过求解下式: \begin{equation} \min_{j,s} = [\min_{c_1}\sum_{x_i\in R_1(j,s))}(y_i-c_1)^2 + \min_{c_2}\sum_{x_i\in R_2(j,s))}(y_i-c_2)^2] \end{equation} 第一层从0~J遍历输入变量$j$,第二层遍历特定变量$j$的数值切分点$s$,得到使上式值最小的对$(j,s)$
- 用选定的对$(j,s)$划分区域: \begin{equation} R_1(j,s) = \{x|x^{(j)}\le s\},R_2(j,s) = \{x|x^{(j)}> s\} \end{equation} 决定两个子区域$\hat c_1$和$\hat c_2$的输出值: \begin{equation} \hat c_m = \frac{1}{N_m}\sum_{x_i\in R_m(j,s)}y_i,x\in R_m, m=1,2 \end{equation}
- 对两个子区域递归调用步骤1和2,直到满足停机条件
- 最终将输入空间划分为$M$个区域$R_1,R_2,…,R_M$,生成决策树: \begin{equation} f(x) = \sum_{m=1}^{M}\hat c_m I (x\in R_m) \end{equation}
CART分类树
特征选择准则
Gini指数
假设有$K$个类别,样本点属于第$k$类的概率为$p_k$,则概率分布的基尼指数为: \begin{equation} Gini(p) = \sum_{k=1}^{K}p_k(1-p_k) = 1 - \sum_{k=1}^{K}p^2_k \end{equation} 对于给定的样本集合$D$,Gini指数为:
\begin{equation} Gini(D) = 1 - \sum_{k=1}^{K}(\frac{|C_k|}{|D|})^2 \end{equation}
其中$C_k$是$D$中属于第$k$类的样本子集,$K$为类别数量
若集合$D$根据特征$A$的取值$a$划分为$D_1$和$D_2$,此时集合$D$的基尼指数定义为: \begin{equation} Gini(D,A) = \frac{|D_1|}{D}Gini(D_1) + \frac{|D_2|}{D}Gini(D_2) \end{equation} 表示经$A=a$分割后集合$D$的不确定性
基尼指数是经验熵公式在$x=1$时的一级泰勒展开,可以理解为经验熵的一种近似
Towing准则
Breiman(CART作者之一)指出,基尼指数在特征的值范围比较宽时会遇到问题,因此引入了一种叫towing准则的二元分类标准$^{[1]}$,其定义如下图所示:
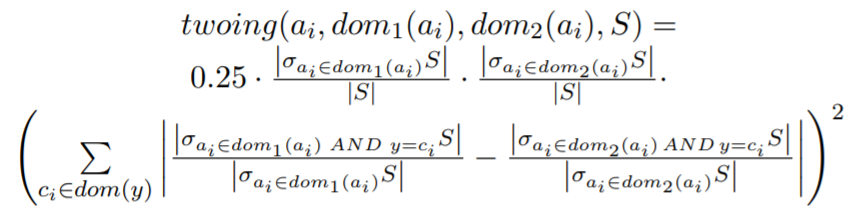
当特征只有二值的时候,gini指数和twoing准则相等;在多分类场景下,twoing准则倾向于选择区分间隔趋于平均的特征;例如四分类场景下,某特征值范围为0~1,第一类为0~0.25,第二类为0.25~0.5..
生成步骤
- 对每一特征$A$,对其每一可能取值$a$,计算$A=a$的gini指数;
- 选择1计算得到的最小gini作为最优特征和最优切分点;
- 根据最优特征和最优切分点划分两个子结点并重新分配子训练集,对两个子结点递归调用1和2;
- 达到停机条件,生成CART分类树。
CART剪枝算法
CART剪枝算法同前文提到的剪枝算法类似,从完全生长的决策树底部开始剪去部分子树,简化决策树。
子树序列
根据损失函数$C_a(T) = C(T)+\alpha|T|$,递归地剪枝:
- 将$\alpha$从小逐渐增大,产生区间$[\alpha_i,\alpha_{i+1}),i=0,1,…,n$;
- 得到对应的子树序列${T_o,T_1,…T_n}$;
- 从$T_o$开始剪枝,对于内部每一结点$t$,计算 \begin{equation} g(t) = \frac{C(t) - C(T_t)}{|T_t| = 1} \end{equation} 上式表示剪枝后整体损失函数减少的程度
- 在$T_o$中剪去$g(t)$最小的$T_t$,将得到的子树作为$T_1$,同时将最小的$g(t)$设为$\alpha_1$,$T_1$即为区间$[\alpha_1,\alpha_2)$的最优子树;
- 继续循环剪枝,直到得到根结点。
交叉验证
利用独立的验证数据集,基于最小平方误差或基尼指数在子树序列${T_o,T_1,…T_n}$中选取最优子树$T_a$
