LTR(Learning To Rank)是有监督的排序学习方法,可应用于信息检索,问答系统,推荐系统商品/用户排序,机器翻译结果排序等诸多领域。RankNet、LambdaMart等经典排序方法的理论成熟,应用广泛,值得深入理解和分析
问答(QA)系统架构简介
功能模块
- Index
- 用于存储QA对的检索库
- Matching Models
- 用于给QA对进行打分的模型,可以包括W2v/N-gram/TF-IDF/BM25/Rnn/Cnn等模型,各类模型对每一个QA对输出一个打分。可以理解为Rank阶段的特征工程。
- Ranking Model
- 排序模型,用于特征融合,多采用树模型或神经网络模型。实际上是一个回归问题。
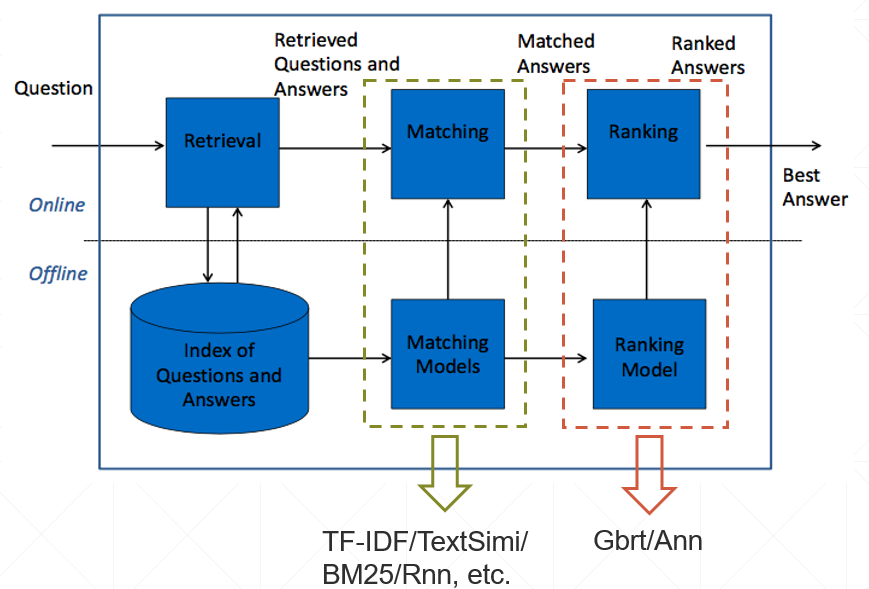
检索过程
- 由于检索库的QA对数量庞大,需要先使用轻量的检索工具返回一定数量的QA对,然后送入Matching models中进行打分。
- Matching models进行打分,构造特征向量。
- Ranking model对向量化的多个QA对进行排序,输出得分最高的QA对作为答案。
Ranking Model类型
以下称每个QA对为一个doc
- Point-wise
将每个doc作为一个instance,采用分类或回归的方法进行训练;缺点是忽略了doc之间的排序关系 - Pair-wise
将每两个doc作为一个instance,考虑其偏序关系 - List-wise
将doclist整体作为一个instance进行训练
训练数据构造
- 给定Matching Models
- 对某一query进行检索将得到有序的doclist。此doclist可按照某重要特征进行粗排序
- 对当前doclist进行人工标注。label表示doc和query的相关程度,数值越大越相关

RankNet
RankNet是一种Pairwise的ranking model,使用神经网络进行学习。RankNet由微软研究院的Chris Burges等人在2005年ICML上的一篇论文Learning to Rank Using Gradient Descent中提出。
定义
\begin{align}
&S_{ij}\in{0,\pm1} \
1&: doc_i比doc_j更相关 \
0&: 同样相关 \
-1&:doc_j比doc_i更相关
\end{align}
假设RankNet训练的任意时刻,模型对$doc_i$和$doc_j$的打分分别为:
\begin{align}
&S_i=f(x_i) \
&S_j=f(x_j) \
x_i和x_j&分别为各自doc的特征向量
\end{align}
模型认为$doc_i$比$doc_j$更相关的概率为
\begin{equation}
P_{ij}\equiv P(U_i\triangleright U_j)\equiv \frac{1}{1+e^{-\sigma(S_i-S_j)}}
\end{equation}
实际$doc_i$比$doc_j$更相关的概率为
\begin{align}
\bar{P_{ij}} &= \frac{1}{2}(1+S_{ij}) \
1&:doc_i比doc_j更相关\
\frac{1}{2}&:同样相关\
0&:doc_j比doc_i更相关
\end{align}
交叉熵损失函数
\begin{equation} C = -\bar{P_{ij}}\log_{}P_{ij}-(1-\bar{P_{ij}})\log_{}(1-P_{ij}) \end{equation} 代入$P_{ij}$和$\bar{P_{ij}}$: \begin{equation} C = \frac{1}{2}(1-S_ij)\sigma(s_i-s_j)+\log(1+e^{-\sigma(s_i-s_j)}) \end{equation}
即使两个doc的得分相同(模型初始化时),若label不同,此时损失$c=\log_{}2$,依然会根据label分别向上下调整排序
求导得到梯度
\begin{align} \frac{\partial{C}}{\partial{s_i}} = \sigma(\frac{1}{2}(1-S_{ij})-\frac{1}{1+e^{\sigma(s_i-s_j)}}) = -\frac{\partial{C}}{\partial{s_j}} \end{align} 梯度大小相等,方向相反
更新网络参数
\begin{equation} w_k \to w_k - \eta\frac{\partial{C}}{\partial{w_k}} = w_k - \eta(\frac{\partial{C}}{\partial{s_i}}\frac{\partial{s_i}}{\partial{w_k}} + \frac{\partial{C}}{\partial{s_j}}\frac{\partial{s_j}}{\partial{w_k}}) \end{equation}
以上为$doc_i$和$doc_j$这一doc pair的参数更新过程,而这样的pair有$n+(n-1)+…+1$对。更新一次参数开销显然过大,能否直接得到$doc_i$的梯度,减少更新次数从而加快训练速度呢?
改写求导公式
\begin{align}
\frac{\partial{C}}{\partial{w_k}} &= \frac{\partial{C}}{\partial{s_i}}\frac{\partial{s_i}}{\partial{w_k}} + \frac{\partial{C}}{\partial{s_j}}\frac{\partial{s_j}}{\partial{w_k}} = \sigma(\frac{1}{2}(1-S_{ij})-\frac{1}{1+e^{\sigma(s_i-s_j)}})(\frac{\partial{s_i}}{\partial{w_k}} - \frac{\partial{s_j}}{\partial{w_k}}) \
&= \lambda_{ij}(\frac{\partial{s_i}}{\partial{w_k}} - \frac{\partial{s_j}}{\partial{w_k}})
\end{align}
定义
\begin{equation}
\lambda_{ij} \equiv \frac{\partial{C}(s_i-s_j)}{s_i} = \sigma(\frac{1}{2}(1-S_{ij})-\frac{1}{1+e^{\sigma(s_i-s_j)}})
\end{equation}
$w$参数的改变量 \begin{equation} \delta{w_k} = - \eta \sum_{\{i,j\}\in{I}}(\lambda_{ij}\frac{\partial{s_i}}{\partial{w_k}} - \lambda_{ij}\frac{\partial{s_j}}{\partial{w_k}}) \equiv - \eta\sum_{i}\lambda_i \frac{\partial{s_i}}{\partial{w_k}} \end{equation} 上式提取出$\lambda_i$,针对的是每个doc而非原求导公式的doc pair \begin{equation} \lambda_i = \sum_{j:\{i,j\}\in{I}} - \sum_{j:\{j,i\}\in{I}} \end{equation} 上式第一项为lambda梯度的“正贡献”项,代表$doc_i$比$doc_j$更相关;第二项为“负贡献”项,代表$doc_j$比$doc_i$更相关
lambda梯度的提出将RankNet的训练时间从接近$𝑂(𝑛^2)$降低为$𝑂(𝑛)$,同时也为LambdaMart模型奠定了基础
不足之处
RankNet的优化方向为降低pair-wise error,并不关心最相关的doc是否排在最前面

RankNet优化过程可能如上图所示
- 左边的doc list共有13个pair-wise error,右边共有11个pair-wise error RankNet可能会进行从左到右的“优化”
- 优化右边的doc list时,RankNet的梯度大小类似于黑色箭头, 而我们更需要红色箭头那样的梯度大小
如何给出更关心相关doc排最前面的优化方向? 加入ranking quality measures!
Ranking Quality Measures
经典的排序评价指标有f1 score/accuracy/AUC/MAP/MRR/DCG/NDCG等,我们重点来看DCG和NDCG两个评价指标
- DCG(Discounted Cumulative Gain)
\begin{equation} DCG@T \equiv \sum_{i=1}^{T}\frac{2^{l_i}-1}{\log_{}(1+i)} \end{equation} $T$为doc list长度,$l_i$为$doc_i$的label,$i$为doc的排名 - NDCG(N-Discounted Cumulative Gain)
\begin{equation}
NDCG@T \equiv \frac{DCG@T}{maxDCG@T}
\end{equation}
此指标将DCG归一化到$(0,1]$ - 指标效果
回到上图,比较左右两个排序结果的dcg指标: \begin{align} dcg_{left} &= \frac{1}{\log{}2} + \frac{1}{\log{}16} = 1.44 + 0.36 = 1.8 \
dcg_{right} &= \frac{1}{\log{}5} + \frac{1}{\log{}12} = 0.62 + 0.40 = 1.02 \end{align}可以看到根据dcg指标,从左到右进行的是“负优化”。如果可以用dcg指标指导梯度下降的方向,那么我们就能看到期待的优化效果
LambdaMart
LambdaMart是LambdaRank的加性多回归树版本,其中MART是Multiple Additive Regression Tree的简称;LambdaMart是基于RankNet发展而来的
定义
给定doc pair $doc_i > doc_j$,假设其效用函数为$C$,定义它的梯度如下: \begin{equation} \lambda_{ij} = \frac{\partial{C}(s_i-s_j)}{\partial{s_i}} = \frac{-\sigma}{1+e^{\sigma(s_i-s_j)}}|\triangle{NDCG}| \end{equation}
- 上式的$|\triangle{NDCG}|$为交换$doc_i$和$doc_j$位置产生的ndcg差值
- 上式的$\frac{-\sigma}{1+e^{\sigma(s_i-s_j)}}$实际是下式当$S_{ij}=1$时的形式
\begin{equation} \lambda_{ij} \equiv \frac{\partial{C}(s_i-s_j)}{\partial{s_i}} = \sigma(\frac{1}{2}(1-S_{ij}) - \frac{1}{1+e^{\sigma(s_i-s_j)}}) \end{equation}
每个doc pair会产生数值相等,方向相反的梯度。对于$doc_i$,计算所有与之label不同的doc贡献给它的梯度,相加得到$doc_i$的梯度 \begin{equation} \lambda_i = \sum_{j:\{i,j\}\in{I}} - \sum_{j:\{j,i\}\in{I}} \end{equation}
Ranking model需要拟合的就是此lambda梯度
lambda梯度例子
假设模型初始化时给分都为0
| 排名 | 特征向量 | label | 模型得分 |
|---|---|---|---|
| doc1 | [feat1,feat2,…featN] | 1 | 0 |
| doc2 | [feat1,feat2,…featN] | 2 | 0 |
| doc3 | [feat1,feat2,…featN] | 1 | 0 |
设$\sigma=1$,同时有模型得分$s_i = s_j$,则下式成立 \begin{equation} \lambda_{ij} = - \frac{\sigma}{1+e^{\sigma(s_i-s_j)}}|\triangle{NDCG}| = -\frac{1}{2}|\triangle{NDCG}| \end{equation}
根据下式
\begin{equation}
|\triangle{dcg}| = |dcg(ori) - dcg(swap)|
\end{equation}
计算得到
\begin{align}
|\triangle{dcg(doc1,doc2)}| &= |(\frac{2^1-1}{\log{}2} + \frac{2^2-1}{\log{}3} + \frac{2^0-1}{\log{}4}) - (\frac{2^2-1}{\log{}2} + \frac{2^1-1}{\log{}3} + \frac{2^0-1}{\log{}4})| \
&= |4.173 - 5.238| \
&= 1.065 \
|\triangle{dcg}(doc1,doc3)| &= 0.721 \
\lambda_1 &= \lambda_{13} - \lambda_{21} = \frac{1}{2}(0.721 - 1.065) = -0.344 \
\lambda_2 &= \lambda_{21} + \lambda_{23} = 0.816 \
\lambda_3 &= -\lambda_{13} - \lambda_{23} = -0.64
\end{align}
此时Mart需要拟合的实际是下表
| 特征向量 | lambda梯度 |
|---|---|
| [feat1,feat2,…featN] | -0.344 |
| [feat1,feat2,…featN] | 0.816 |
| [feat1,feat2,…featN] | -0.64 |
lambda梯度优化方向
Mart在函数空间进行梯度下降,拟合的正好是损失/效用函数对模型得分的梯度,很自然地将lambda梯度和mart结合起来
根据梯度反推效用函数$C$
\begin{equation}
C = \sum_{{i,j}\rightleftharpoons{I}}|\triangle{Z_{ij}}|\log{}(1+e^{-\sigma(s_i-s_j)})
\end{equation}
此时有:
\begin{equation}
\frac{\partial{C}}{\partial{s_i}} = \sum_{{i,j}\rightleftharpoons{I}} \frac{-\sigma|\triangle{Z_{ij}}|}{\log{}(1+e^{\sigma(s_i-s_j)}} \equiv \sum_{{i,j}\rightleftharpoons{I}} -\sigma|\triangle{Z_{ij}}|\rho_{ij}
\end{equation}
$\triangle{Z_{ij}}$可以理解为交换$doc_i$和$doc_j$位置后产生的评价指标差值(可以直接理解为NDCG差值)
其中: \begin{equation} \rho_{ij} \equiv \frac{1}{\log{}(1+e^{\sigma(s_i-s_j)}} = \frac{-\lambda_{ij}}{\sigma|Z_{ij}|} \end{equation}
拟合lambda梯度,实际上是使用梯度上升对效能函数$C$进行优化
Mart输出值计算
- 首先设置每棵树的最大叶子数,基分类器通过最小平方损失进行分裂,达到最大叶子数量时停止分裂
- 使用牛顿法得到叶子的输出,计算效用函数对模型得分的二阶导$\frac{\partial{\lambda_i}}{\partial{s_i}} = \frac{\partial^{2}{C}}{\partial^{2}{s_i}}$ \begin{equation} \frac{\partial^{2}{C}}{\partial^{2}{s_i}} = \sum_{\{i,j\}\rightleftharpoons{I}} \sigma^2 |\triangle{Z_{ij}}| \rho_{ij} (1-\rho_{ij}) \end{equation}
- 得到第m颗树的第k个叶子的输出值 \begin{equation} \gamma_{km} = \frac{\sum_{x_i\in{R_{km}}}\frac{\partial{C}}{\partial{s_i}}}{\sum_{x_i\in{R_{km}}}\frac{\partial^{2}{C}}{\partial^{2}{s_i}}} = \frac{-\sum_{x_i\in{R_{km}}}\sum_{\{i,j\}\rightleftharpoons{I}}|\triangle{Z_{ij}}| \rho_{ij}}{\sum_{x_i\in{R_{km}}}\sum_{\{i,j\}\rightleftharpoons{I}}|\triangle{Z_{ij}}| \sigma \rho_{ij}(1-\rho_{ij})} \end{equation}
- $x_i$为第$i$个样本,$x_i\in{R_{km}}$意味着落入该叶子的样本,这些样本共同解决了该叶子的输出值
流程总结

可以看到整个过程和普通的Gbrt算法几乎一致,主要的差异就是标红处拟合的$y_i$是lambda梯度$\lambda_i$
